Introduction
Machine learning is one of the most exciting aspects of computer science because it allows us to experiment with problem solving skills performed by a computer without the programmer hard wiring the steps needed to come up with a solution. A while back we explored the use of genetic algorithms to solve numerical problems. In this article I would like to discuss another offshoot of the genetic algorithm called Population Based Incremental Learning (PBIL).
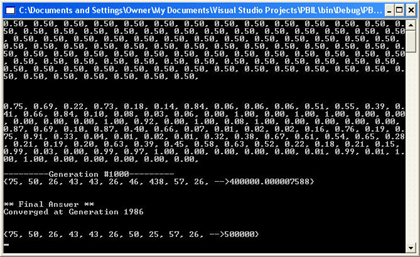
Figure 1 - The Results of a PBIL algorithm on finding the points on a Circle with radius 25 and center 50,50
Population Based Incremental Learning
PBIL allows you to represent your entire genetic population base through a probability vector rather than a myriad of chromosomes. A probability vector is simply a sequence of probabilities. Each probability value in the sequence represents the probability that we can generate a 1 or 0 at the gene position. For example the probability vector {.5, .5, 1, 1} can be represented by the following population
{0, 0, 1, 1}
{0, 1, 1, 1}
{1, 0, 1, 1}
{1, 1, 1, 1}
The probability that we will generate a 1 or 0 in the first position is 50/50, so 50% of the chromosomes in the population have 1 in the first position, and 50% of the chromosomes in the population have 0 in the first position. The probability of generating a one in the 3rd and 4th position is 1, so this number will always be one.
The algorithm for generating a solution using probability vectors is actually quite simple.
1. Initialize a probability vector with all probabilities being 1/2.
2. Generate a population of N chromosomes using the probability vector to randomly determine the gene in each chromosome position (1 or 0).
3. Evaluate the fitness of each chromosome based on a fitness function for your particular problem
4. Sort all chromosomes by fitness value
5. Update the probability value in each vector position based on the top X chromosomes using a learning rate.
Probability Vector := Probabilty Vector * (1.0 - LR) + topchromosome* (LR);
where LR = some learning rate
6. Check to see if the probability vector has converged. If not, repeat steps (2) through (5)
Listing 1 - PBIL Algorithm Steps
This algorithm is much easier to implement than the simple genetic algorithm (which involves crossovers, mutations, reproductions, and deaths), but is actually just as effective. It's a better algorithm in that it doesn't require you to remember as much information from generation to generation. You only need to maintain the probability vector which contains the probability distribution of each gene in our chromosome.
The Design
Below is the simple UML Design used by our algorithm implementation. The BinaryGene class has five methods that aid us in our PBIL implementation: CalculateFitness, CompareTo, UpdateProbabilityVector, and HasConverged. CalculateFitness is the method that we use to calculate our fitness function. The higher the value returned from this method, the higher the fitness of the chromosome. CompareTo implements the IComparable interface to allow us to sort Genomes by fitness. UpdateProbabilityVector modifies the probability vector in our algorithm according to the learning rate and the genes in our highest fit chromosomes. The HasConverged method determines if the probability vector has converged to a final solution with all 1's and 0's.
Note that the chromosome contains an array of integers called _genome. This array will either contain a value of 0 or 1. The Generate method of the BinaryGene class allows us to generate a chromosome based on the probability vector. The FormNumber method is used to break down the binary 1's and 0's inside the genome into integer values for use in the fitness function. Finally, the ToString method allows us to write our gene to the console as a readable string of integer values.
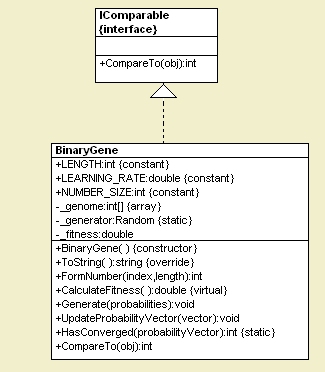
Figure 2 - Chromosome for PBIL Algorithm reverse engineered using WithClass UML Tool
Implementing PBIL through the Binary Gene Class
Once we've created our class to handle all major steps of the PBIL algorithm, we can easily implement our algorithm. Listing 2 shows the step by step implementation of PBIL through the binary gene class.
[STAThread]
static void Main(string[] args)
{
BinaryGene[] _genomes = new BinaryGene[NUMBER_OF_SAMPLES];
double[] _probabilities = new double[BinaryGene.LENGTH];
// (1) generate initial probability vector
for (int i = 0; i < BinaryGene.LENGTH; i++)
{
_probabilities[i] = .5d; // initialize probabilities
}
// (2) generate chromosomes based on probability vector
// (3) calculate fitness of each gene
for (int i = 0; i < NUMBER_OF_SAMPLES; i++)
{
_genomes[i] = new BinaryGene();
_genomes[i].Generate(_probabilities);
_genomes[i].CalculateFitness();
}
// (4) Sort all chromosomes by fitness value
Array.Sort(_genomes);
// (5) Update the probability value in each vector position based on the top X chromosomes using a learning rate
for (int i = 0; i < NUMBER_OF_VECTORS_TO_UPDATE_FROM; i++)
{
_genomes[i].UpdateProbabilityVector(_probabilities);
}
// (6) Check to see if the probability vector has converged.
// If not, repeat steps (2) through (5)
// else we are finished
int convergenceFailureIndex = BinaryGene.HasConverged(_probabilities);
if (convergenceFailureIndex < 0)
{
Console.WriteLine("** Final Answer **");
Console.WriteLine("Converged at Generation {0}", counter);
break;
}
}
Console.WriteLine(_genomes[0].ToString()); // this is the final genome after convergence or 20,000th generation
Console.ReadLine();
}
Listing 2 - PBIL Implementation of the BinaryGene class
Experimenting with Fitness Functions
Once the algorithm is in place, we can test it on different fitness functions to produce different solutions. The first fitness function we will use to test PBIL is the fitness for a Fibonacci sequence. The Fibonacci sequence is a sequence of numbers whose previous two numbers in the sequence sum to produce the current number. The fitness function for this sequence is shown below:
///
<summary>
/// Find a Fibonacci sequence where x(i+2) = x(i) + x(i+1)
/// </summary>
void FindFibonacci()
{
// track the previous number, and the number before
// the previous number
int _previousNumber = 1;
int _previousPrevious = 0;
// cycle through each groups of bits in the chromosome
for (int i = 0; i < LENGTH; i+=NUMBER_SIZE)
{
// form integer value from ones and 0's in the chromosome
// at the i-th position
int nextNumber = FormNumber(i, NUMBER_SIZE);
// fitness is if the sum of the previous two numbers
// equals the current number. The farther away the sum is
// from current number, the lower the fitness
_fitness = _fitness + Math.Exp( - (Math.Abs((nextNumber - (_previousNumber + _previousPrevious) ))));
_previousPrevious = _previousNumber;
_previousNumber = nextNumber;
}
if (_previousNumber > 500) // limit values to less than 500 by reseting the fitness
{
_fitness = 0;
}
}
Listing 3 - Fibonacci Fitness Function
After running the PBIL algorithm on the fitness function above, the result produces a perfect Fibonacci sequence at generation 1986 shown in figure 3. Note that if you split the probability vector into groups of 10 bits, the first bit being the least significant, it will match the final solution produced in the fittest chromosome.
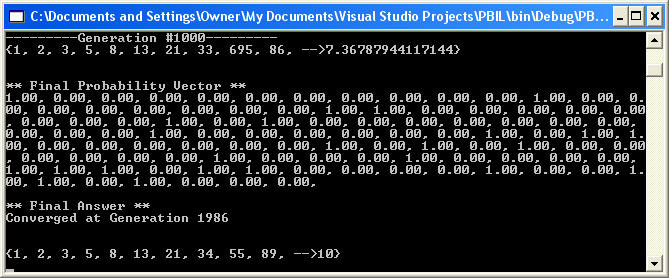
Figure 3 - Fibanocci Sequence Solution Produced from PBIL
A more complicated fitness function we tried on PBIL is a function to test for perfect number factors. A perfect number is a number whose factors produce a sum of the same number. For example, the factors of the number 6 are 1,2, and 3.
(1)(2)(3) = (1+2+3) = 6. So 6 is a perfect number.
Below is the fitness function we used to find a set of factors for a perfect number. The fitness function looks for a product and sum that match. It also looks for other criteria such as only one factor of the number 1:
/// <summary>
/// Find a perfect number using PBIL
/// </summary>
/// <returns></returns>
double CalculatePerfectNumber()
{
double sum = 0;
double product = 1;
int nextNumber = 0;
bool oneThere = false;
int moreThanOneNonZero = 0;
int moreThanOneOne = 0;
// go through each number in the chromosome
for (int i = 0; i < LENGTH; i+=NUMBER_SIZE)
{
// form integer from binary representation
nextNumber = FormNumber(i, NUMBER_SIZE);
if (nextNumber == 1)
{
oneThere = true; // always need a one.
moreThanOneOne++; // don't want more than one 1
}
// track all non-zero numbers
if (nextNumber != 0)
{
moreThanOneNonZero++;
}
// compute the sum of factors
sum = sum + nextNumber;
// compute the sum of all non-zero factors
if (nextNumber != 0)
{
product = product * nextNumber;
}
}
// fitness is roughly 1/ (product - sum)
// the closer the sum is to the product,
// the greater the fitness
_fitness = 1.0d/(Math.Abs(product - sum)*10000.0d + .0000001);
// don't count infinite answers
if (product == double.NaN)
{
_fitness = -100000;
}
// all perfect numbers have 1 as a factor
// so make sure we have one
if (!oneThere)
{
_fitness = 0;
}
// can't have more than one one as a factor
if (moreThanOneOne > 1)
{
_fitness = 0;
}
// must have at least 2 non-zero factors (which can include 1)
if (moreThanOneNonZero < 2)
{
_fitness = 0;
}
return _fitness;
}
The results of the perfect number fitness function are shown below in figure 4. Note that the factors for 6 are produced:
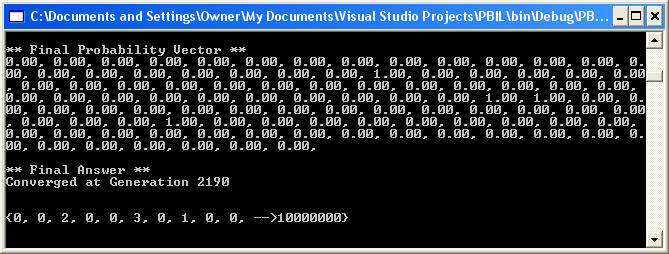
Figure 4 - Results of PBIL run on a Fitness Function for finding Perfect Number Factors
Conclusion
Genetic Algorithms are a powerful tool in which computers can be used to solve problems without programmer knowledge. PBIL is a variation of iterative learning algorithm that performs as well as a genetic algorithm and is easier to implement and more compact for saving solution information from iteration to iteration. In this article we used PBIL to solve some simple math problems. However, you can expand PBIL to solve real world problems in fields such as chemistry, economics, and mechanics. In our next AI article we will examine a similar algorithm called the Compact Genetic Algorithm (cGA).
References