Edited by Nina Miller
Introduction
It always amazes me how effective the process of trial and error is at reaching the desired solution. Genetic Algorithms are trial and error in its purest form, each generation getting closer and closer to the solution defined by a given set of fitness parameters. This article combines the CodeDOM Calculator with the Compact Genetic Algorithm to create a root solving application. Using this application, you can type in any polynomial, and the genetic algorithm will attempt to converge on the best solution for the equation. The solution can be real or complex. Below is a sample of converging on the solution to the equation:
x2 + 2x + 10 = 0
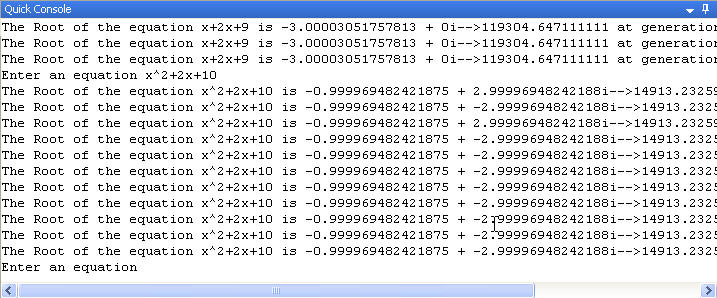
Figure 1 - Running GA Root Solver to find the complex roots of the equation x2 + 2x + 10 = 0
Essentially the solution derived by the Compact GA was (-1 ± 3i). Let's test this solution with one of the roots (-1 +3i):
= (-1 + 3i)(-1 + 3i) + 2(-1 + 3i) + 10
= (1 - 9 -6i) + (-2 + 6i) + 10
= (1 - 9 - 2) + (-6i + 6i) + 10
= -10 + 0 + 10
= 0
Let's even try a more difficult equation:
x4 - 7x2 + 14x + 25 = 0
The GA Solver converges on a solution fairly quickly:
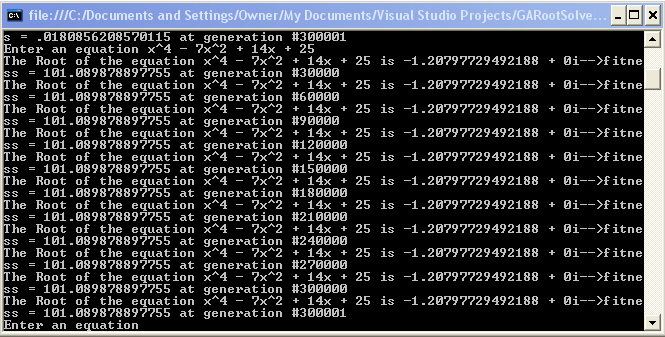
Figure 2 - Running GA Root Solver to find the complex roots of the equation x4 - 7x2 + 14x + 25 = 0
Again testing our GA solution:
= (-1.20797729492188)4 - 7(-1.20797729492188)2 + 14(-1.20797729492188) + 25
= 2.129291328988 - 10.2144640153275 + -16.91168212890632 + 25
= -24.997 + 25
= .003
This gives us a solution off by 3/1000. Note that if we compare the fitnesses for the figure 1 solution and the figure 2 solution, figure 1 had a fitness of 14913. Figure 2 had a fitness of approximately 101 which is much lower than figure 1's fitness. The fitness measurement reflects how confident we are of our converged solution.
The Design
The design consists of two namespaces: the CompactGA and the CodeDomStuff. The CompactGA executes a compact genetic algorithm on a BinaryChromosome. Each binary chromosome contains a string of 1's and 0's representing a complex number. Because manipulating complex numbers requires complex math, we've also included a Complex class to handle multiplication, addition, and subtraction of complex numbers.
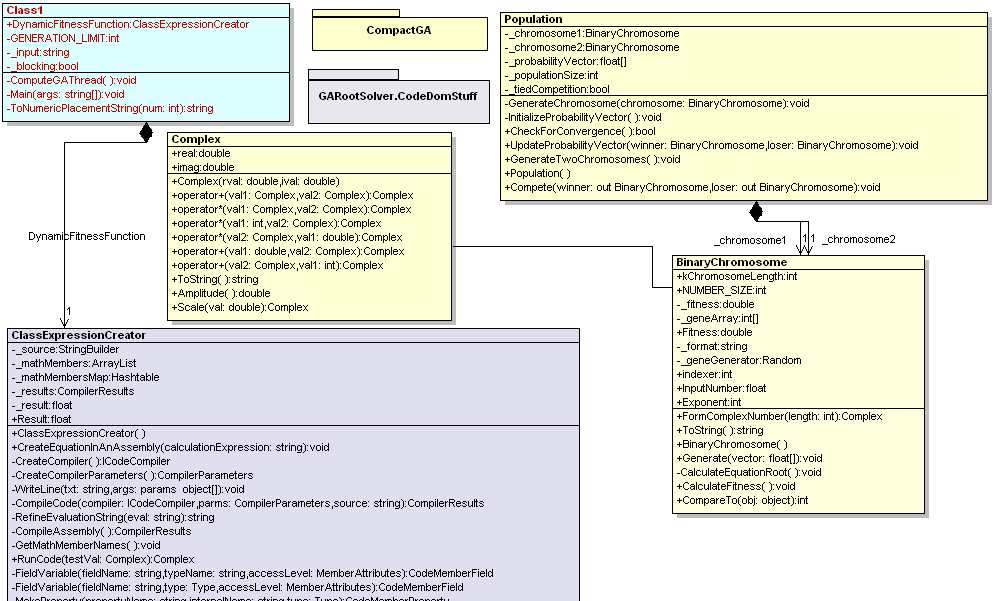
Figure 3 - UML Design of GARootSolver Reverse Engineered from C# using WithClass
Fitness Function
The fitness function in the BinaryChromosome class, CalculateFitness, calls CalculateEquationRoot to determine the fitness of the binary chromosome representing a possible complex root solution. The fitness is determined by plugging the complex chromosome value back into the equation we are trying to solve. The closer the resulting value is to 0, the higher the fitness and the closer to our desired solution.
Listing 1 - Calculating the fitness of the Complex Chromosome
public void CalculateFitness()
{
_format = "f";
CalculateEquationRoot();
}
void CalculateEquationRoot()
{
// form the complex number from the 1's and 0's in the binary array
Complex root = FormComplexNumber(kChromosomeLength);
// plug the chromosome's complex value into the equation
Complex result = Class1.DynamicFitnessFunction.RunCode(root);
// compare the value of the product to the actual input number
// and compute a fitness. a result of 0 in the denominator is best, so a fitness of 1/0 or infinity would be an exact solution
_fitness = 1.0f/Math.Abs((result.real*result.real + result.imag*result.imag) * 1000);
} |
Forming the Complex Number
The complex number is formed by taking the binary chromosome and splitting it into two equal parts: a real binary part and a complex binary part. So for example, if our binary chromosome has the value shown below and we were only dealing in integers:
11000101
Then the resulting complex number would be:
1100 + 0101i
or
12 + 5i
In our case, we want to support fractional values so we scale our binary values by a factor of (2)chromosome_length/4. Our chromosomes are 60 bits long, so the number would be scaled down by 2(60/4) or 215 or 32768. Therefore the above value of 1100 + 0101i would really be equivalent to
12/32768 + 5/32768i or
.00032199 + .000152587
The code for forming the complex number from the binary chromosome is shown in listing 2:
Listing 2 - Forming a complex number from a string of bits
public Complex FormComplexNumber(int length)
{
double result1 = 0;
double result2 = 0;
long real = 0;
long imag = 0;
// compute the real part of the binary chromosome
// in the top half of the binary array
for (int i = 0; i < length/2 - 1; i++)
{
real = real << 1;
real = real + (long)_geneArray[(length - i) - 1];
}
// scale the real part by 2 ^ (genome_length/4)
result1 = (double)real;
long scale = 1L << (length / 4);
result1 = result1 / scale;
// first bit is a sign bit for the real part
if (_geneArray[length/2 + 1] == 1)
{
// negative
result1 = -result1;
}
// compute the imaginary part of the binary chromosome
// in the bottom half of the binary array
for (int i = length / 2; i < length - 1; i++)
{
imag = imag << 1;
imag = imag + (long)_geneArray[(length - i) - 1];
}
// scale the imaginary part by 2 ^ (genome_length/4)
result2 = (double)imag;
scale = 1L << (length / 4);
result2 = result2 / scale;
// first bit is a sign bit for the imaginary part
if (_geneArray[0] == 1)
{
// negative
result2 = -result2;
}
// return a complex number instance formed
// from the real and imaginary binary parts
return new Complex(result1, result2);
} |
Equation Input Features
As in our CodeDOM Calculator,, we take the input equation string from the user and refine it so that .NET can compile it dynamically. One of the optimizations we make is to allow the user to enter x^3 as opposed to x*x*x. Therefore, internally, we need to make the change before it reaches the compiler. The method RefineEvaluationString in the ClassExpressionCreator shows some of the substitutions we need to make before compiling the code dynamically using CodeDOM.
Listing 3 - Refining our input equation to make it compileable
string RefineEvaluationString(string eval)
{
// look for regular expressions with only letters
Regex regularExpression = new Regex("[a-zA-Z_]+");
// track all functions and constants in the evaluation expression we already replaced
ArrayList replacelist = new ArrayList();
// find all alpha words inside the evaluation function that are possible functions
MatchCollection matches = regularExpression.Matches(eval);
foreach (Match m in matches)
{
// if the word is found in the math member map, add a Math prefix to it
bool isContainedInMathLibrary = _mathMembersMap[m.Value.ToUpper()] != null;
if (replacelist.Contains(m.Value) == false && isContainedInMathLibrary)
{
// substitute the static math method
eval = eval.Replace(m.Value, "Math." + _mathMembersMap[m.Value.ToUpper()]);
}
// we matched it already, so don't allow us to replace it again
replacelist.Add(m.Value);
}
Regex regularExpression2 = new Regex("[0-9]x");
// find all matches of type <number>x
matches = regularExpression2.Matches(eval);
string evalOld = eval;
int count = 0;
// replace all occurrences <number>x with <number> * x so .NET can compile it
foreach (Match m in matches)
{
count++;
// replace the evaluation string that will be converted to .NET code with compilable code
eval = eval.Substring(0, m.Index + count) + "*" + eval.Substring(m.Index + count);
}
// find all matches of type x ^<number>
Regex regularExpression3 = new Regex(@"x\^[0-9\.\-]+");
matches = regularExpression3.Matches(eval);
// replace all occurrences of x^<number> with x*x*...
foreach (Match m in matches)
{
count++;
string replaceString = "x";
for (int i = 0; i < Convert.ToInt32(m.Value.Substring(m.Value.IndexOf("^") + 1)) - 1; i++)
{
replaceString = replaceString + "*x";
}
// replace the evaluation string that will be converted to .NET code with compilable code
eval = eval.Replace(m.Value, replaceString);
}
// return the modified evaluation string
return eval;
} |
Conclusion
Genetic Algorithms give us a powerful way to test possible solutions to complex equations and quickly converge onto a final solution. CodeDom allows to dynamically create compiled code containing the equation we wish to test and use this code in the method of our fitness function. Together, we used these two technologies to create a GA Root Solver that allowed us to input a polynomial equation and find the complex root. In testing this program, we found that the GA performed best with equation containing complex solutions with magnitudes between 0 and 1. Feel free to experiment with the code in this download. Perhaps you will find other ways to refine the input or improving upon the genetic algorithm. Either way, we trust that you will get to the root of the problem you are trying to solve with C# and .NET.
Other GA Algorithm Articles by the Author:
Implementing a Genetic Algorithm in C#
CodeDom Calculator
AI: Using the Compact Genetic Algorithm to Compute Square Roots in C#