SQL Operations

Introduction An operation is an action performed on one or more values either to modify the value held by one or both of the variables or to produce a new value by combining values. Therefore, an operation is performed by using at least one symbol and one value. The symbol used in an operation is called an operator. A value involved in an operation is called an operand. PRINT Something Like every language, SQL ships with some words used to carry its various operations. One of these words is PRINT. To display something in plain text as a result of a statement, type PRINT followed by what to display. Therefore, PRINT uses the following formula: PRINT WhatToPrint The item to display can be anything that is allowed and it is provided on the right side of PRINT. If it is a regular constant number, simply type it on the right side of PRINT. 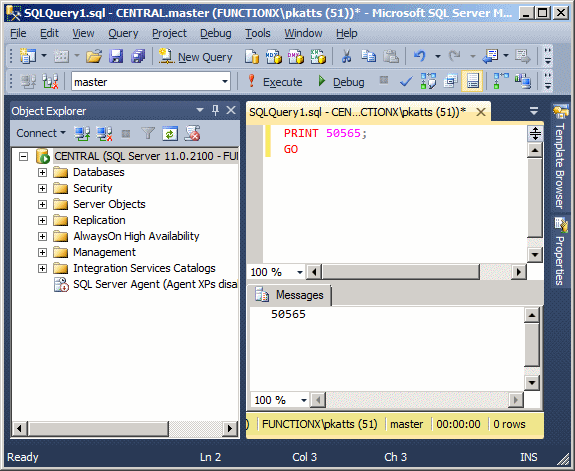Here is an example: The item to display can also be an operation or the result of an operation. If you want to display a character, a word, or a sentence, include it between single-quotes. If you want to include a single-quote in your statement, double it; that is, write it twice. Here is an example: You can also display an expression as a combination of number(s) and sentences as we will learn later. SELECT   SELECT Anything The SELECT operator can be used, among other things, to display a value. The SELECT keyword uses the following syntax: SELECT What Based on this, to use it, where it is needed, type SELECT followed by a number, a word, a string, or an expression. The item to display follows some of the same rules as PRINT. One of the differences between PRINT and SELECT is that: PRINT is mostly used for testing a simple value, a string, or an expression. Therefore, it displays its results in a regular white window under a tab labeled Messages. PRINT can be used with only one value SELECT is the most regularly used SQL operator. We will see that it is used to retrieve records from a table. For this reason, SELECT displays its results in an organized window made of categories called columns, under a tab labeled Results. SELECT can be used with more than one value As done for PRINT, to display a sentence using SELECT, type it in single-quotes on the right side of this operator. Here is an executed example: As mentioned already, unlike PRINT, SELECT can be used to display more than one value. The values must be separated by commas. Here is an example: SELECT 'Hourly Salary', 24.85; This would produce: Nesting a SELECT Statement When you create a SELECT statement, what is on the right side of SELECT must be a value. Here is an example: SELECT 226.75; Based on this definition, instead of just being a value, the thing on the right side of SELECT must be able to produce a value. As we will see in the next sections, you can create algebraic operation on the right side of SELECT. Because we mentioned that the thing on the right side must produce a result, you can as well use another SELECT statement that it itself evaluates to a result. To distinguish the SELECT sections, the second one should be included in parentheses. Here is an example: SELECT (SELECT 448.25); GO When one SELECT statement is created after another, the second is referred to as nested. Just as you can nest one SELECT statement inside of another, you can also nest one statement in another statement that itself is nested. Here is an example: SELECT (SELECT (SELECT 1350.75)); GO SELECT This AS That In the above introductions, we used either PRINT or SELECT to display something in the query window. One of the characteristics of SELECT is that it can segment its result in different sections. SELECT represents each value in a section called a column. Each column is represented with a name also called a caption. By default, the caption displays as "(No column name)". If you want to use your own caption, on the right side of an expression, type the AS keyword followed by the desired caption. The item on the right side of the AS keyword must be considered as one word. Here is an example: SELECT 24.85 AS HourlySalary; This would produce: You can also include the item on the right side of AS in single-quotes. Here is an example: SELECT 24.85 AS 'HourlySalary'; If the item on the right side of AS is in different words, you should include it in single-quotes or put them in inside of an opening square bracket "[" and a closing square bracket "]". Here is an example: SELECT 24.85 AS 'Hourly Salary'; If you create different sections, separated by a comma, you can follow each with AS and a caption. 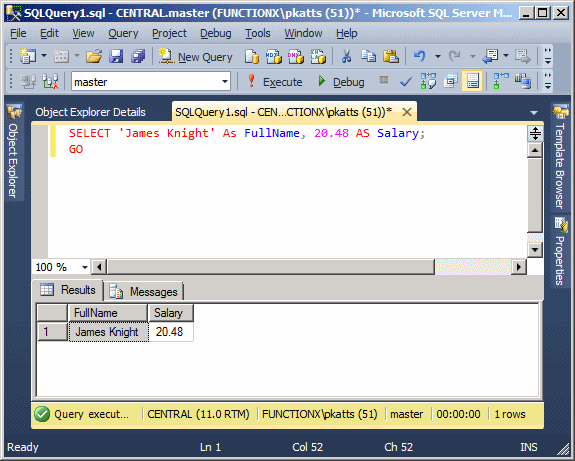Here is an example: SELECT 'James Knight' As FullName, 20.48 AS Salary; This would produce: The above statement could also be written as follows: SELECT 'James Knight' As [Full Name], 20.48 AS [Hourly Salary]; Unary Operators   The Positive Operator + A unary operator is an operator that performs its operation on only one operand. Algebra uses a type of ruler to classify numbers. This ruler has a middle position of zero. The numbers on the left side of the 0 are referred to as negative while the numbers on the right side of the rulers are considered positive: -8   -6 -5 -4 -3 -2 -1   1 2 3 4 5 6   +8    0 -8   -6 -5 -4 -3 -2 -1   1 2 3 4 5 6   +8 A value on the right side of 0 is considered positive. To express that a number is positive, you can write a + sign on its left. Examples are +4, +228, +90335. In this case the + symbol is called a unary operator because it acts on only one operand. The positive unary operator, when used, must be positioned on the left side of its operand, never on the right side. As a mathematical convention, when a value is positive, you do not need to express it with the + operator. Just writing the number without any symbol signifies that the number is positive. Therefore, the numbers +4, +228, and +90335 can be, and are better, expressed as 4, 228, 90335. Because the value does not display a sign, it is referred as unsigned as we learned in the previous lesson. To express a variable as positive or unsigned, you can just type it. here is an example: PRINT +1250 The Negative Operator - As you can see on the above ruler, in order to express any number on the left side of 0, it must be appended with a sign, namely the - symbol. Examples are -12, -448, -32706. A value accompanied by - is referred to as negative. The - sign must be typed on the left side of the number it is used to negate. Remember that if a number does not have a sign, it is considered positive. Therefore, whenever a number is negative, it MUST have a - sign. In the same way, if you want to change a value from positive to negative, you can just add a - sign to its left. Here is an example that uses two variables. One has a positive value while the other has a negative value: SELECT -1250 Binary Operators   The Addition An operator is referred to as binary if it operates on two operands. The addition, also called the sum, is an operation used to add one item to another. The addition is performed using the + sign. To get the addition of two values, you type + between them, as in Value1 to Value2. After the addition has been performed, you get a new value that you can make available or display to the user. You can perform the addition on two numbers. Here is an example: PRINT 125 + 4088 In Transact-SQL, you can also perform the addition on text. Here is an example: PRINT 'Henry ' + 'Kono' You can also add more than two values, like a + b + c. The order you use to add two or more values doesn't matter. This means Value1 + Value2 is the same as Value2 + Value1. In the same way a + b + c is the same as a + c + b the same as b + a + c and the same as c + b + a. The Subtraction The subtraction operation, sometimes called the difference, is used to take out or subtract one value from another value. It is essentially the opposite of the addition. The subtraction is performed with the - sign. Here is an example: PRINT 1240 - 608 Unlike the addition, the subtraction operation is not associative. This means that a - b - c is not necessarily equal to c - b - a. This is illustrated in the following statements: PRINT 128 - 42 - 5 PRINT 5 - 42 - 128 This would produce: 81 -165 Notice that both operations of the addition convey the same result. In the subtraction section, the numbers follow the same order but a different operation; and the last two operations render different results. The Multiplication The multiplication allows adding one value to itself a certain number of times, set by a second value. As an example, instead of adding a value to itself in this manner: a + a + a + a, since the variable a is repeated over and over again, you could simply find out how many times a is added to itself, then multiply a by that number which, is this case, is 4. This would mean adding a to itself 4 times, and you would get the same result. The multiplication is performed with the * sign. Just like the addition, the multiplication is associative: a * b * c = c * b * a. Here is an example: PRINT 128 * 42 This would produce 5376 The Division  The division operation is similar to cutting an item in pieces or fractions of a set value. Therefore, the division is used to get the fraction of one number in terms of another. The division is performed with the forward slash /. Here is an example: PRINT 128 / 42 This would produce 3 When performing the division, be aware of its many rules. Never divide by zero (0). Make sure that you know the relationship(s) between the numbers involved in the operation. The Modulo In the above division, 128/42, the result is 3. When you multiply 42 by 3, as in 42*3, you get 126. In some cases, you may be interested in knowing the amount that was left out after the operation. The modulo operation is used to get the remainder of a division as a natural number. The remainder operation is performed with the percent sign (%). Here is an example: PRINT 128 % 42 This would produce 2. Parentheses Like most computer languages, Transact-SQL uses parentheses to isolate a group of items that must be considered as belonging to one entity. For example, as we will learn soon, parentheses allow a function to delimit the list of its arguments. Parentheses can also be used to isolate an operation or an expression with regards to another operation or expression. For example, when studying the algebraic operations, we saw that the subtraction is not associative and can lead to unpredictable results. In the same way, if your operation involves various operators such as a mix of addition(s) and subtraction(s), you can use parentheses to specify how to proceed with the operations, that is, what operation should (must) be performed first. Here is an example: PRINT (154 - 12) + 8 PRINT 154 - (12 + 8) This would produce: 150 134 As you can see, using the parentheses controls how the whole operation would proceed. This difference can be even more accentuated if your operation includes 3 or more operators and 4 or more operands. Here is another example of a nested SELECT statement that uses parentheses: SELECT (SELECT 448.25 * 3) + (SELECT 82.28 - 36.04); GO   Bit Manipulations   Introduction When you use a value in your database or application, the value must be stored somewhere in the computer memory using a certain amount of space. A value occupies space that resembles a group of small boxes. In our human understanding, it is not always easy to figure out how a letter such as as B is stored in 7 seven small boxes when we know that B is only one letter. Bit manipulation or a bit related operation allows you to control how values are stored in bits. This is not an operation you will need to perform very often, especially not in the early stages of your database. Nevertheless, bit operations (and related overloaded operators) are present in all or most programming environments, so much that you should be aware of what they do or what they offer. Bits Operators: The Bitwise NOT Operator ~ One of the operations you can perform on a bit consists of reversing its value. That is, if a bit holds a value of 1, you may want to change it to 0 and vice-versa. This operation can be taken care of by the bitwise NOT operator that is represented with the tilde symbol ~ The bitwise NOT is a unary operator that must be placed on the left side of its operand as in ~Value Here is an example: PRINT ~158 To perform this operation, the Transact-SQL interpreter considers each bit that is part of the operand and inverts the value of each bit from 1 to 0 or from 0 to 1 depending on the value the bit is holding. This operation can be resumed in the following table: Bit ~Bit 1 0 0 1 Consider a number with a byte value such as 248. In our study of numeric systems, we define how to convert numbers from one system to another. Based on this, the binary value of decimal 248 is 1111 1000 (and its hexadecimal value is 0xF8). If you apply the bitwise NOT operator on it to reverse the values of its bits, you would get the following result:  Value 1 1 1 1 1 0 0 0 ~Value 0 0 0 0 0 1 1 1   Bits Comparison: The Bitwise AND Operator & The bitwise & is a binary operator that uses the following syntax Operand1 & Operand2 This operator considers two values and compares the bit of each with the corresponding bit of the other value. If both corresponding bits are 1, the comparison produces 1. Otherwise, that is, if either bit is 0, the comparison produces 0. This comparison is resumed as follows: Bit1 Bit2 Bit1 & Bit2 0 0 0 1 0 0 0 1 0 1 1 1 Imagine you have two byte values represented as 187 and 242. Based on our study of numeric systems, the binary value of decimal 187 is 1011 1011 (and its hexadecimal value is 0xBB). The binary value of decimal 242 is 1111 0010 (and its hexadecimal value is 0xF2). Let's compare these two values bit by bit, using the bitwise AND operator:   Binary Decimal N1 1 0 1 1 1 0 1 1 187 N2 1 1 1 1 0 0 1 0 242 N1 & N2 1 0 1 1 0 0 1 0 178 Most of the times, you will want the interpreter to perform this operation and use the result in your program. This means that you can get the result of this operation and possibly display it to the user. The above operation can be performed by the following program: PRINT 187 & 242 This would produce 178 Bits Comparison: The Bitwise OR Operator | You can perform another type of comparison on bits using the bitwise OR operator that is represented by |. Its syntax is: Value1 | Value2 Once again, the interpreter compares the corresponding bits of each operand. If at least one of the equivalent bits is 1, the comparison produces 1. The comparison produces 0 only if both bits are 0. This operation is resumed as follows: Bit1 Bit2 Bit1 | Bit2 0 0 0 1 0 1 0 1 1 1 1 1 Once again, let's consider decimals 187 and 242. Their bitwise OR comparison would render the following result:   Binary Decimal N1 1 0 1 1 1 0 1 1 187 N2 1 1 1 1 0 0 1 0 242 N1 | N2 1 1 1 1 1 0 1 1 251 You can also let the compiler perform the operation and produce a result. Here is an example: PRINT 187 | 242 This would produce 251 Bits Comparison: The Bitwise-Exclusive XOR Operator ^ Like the previous two operators, the bitwise-exclusive OR operator performs a bit comparison of two values. It syntax is: Value1 ^ Value2 The compiler compares the bit of one value to the corresponding bit of the other value. If one of the bits is 0 and the other is 1, the comparison produces 1. In the other two cases, that is, if both bits have the same value, the comparison produces 0. This operation is resumed as follows: Bit1 Bit2 Bit1 ^ Bit2 0 0 0 1 0 1 0 1 1 1 1 0 We will again consider decimals 187 and 242. Their bitwise-exclusive XOR comparison would render the following result:   Binary Decimal N1 1 0 1 1 1 0 1 1 187 N2 1 1 1 1 0 0 1 0 242 N1 ^ N2 0 1 0 0 1 0 0 1 73 If the interpreter performs this operation, it can produce a result as in the following example: PRINT 187 ^ 242; This would produce 73.